How Linear Regression Works (Visualized Step-by-Step)

We’ll visualize every step of how Linear Regression works using Python and Matplotlib.

---

📌 What is Linear Regression?

At its core, Linear Regression tries to find the best-fitting straight line through a set of points. This line can be used to predict new values.

The equation of a line is:

python
y = mx + b

Where:

• m is the slope (weight),
• b is the intercept (bias).

---

📊 Step 1: Generate Sample Data

python
import numpy as np
import matplotlib.pyplot as plt

# Generate synthetic data
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# Visualize it
plt.figure(figsize=(16, 9))
plt.scatter(X, y, alpha=0.7)
plt.title("Generated Data")
plt.xlabel("X")
plt.ylabel("y")
plt.grid(True)
plt.show()

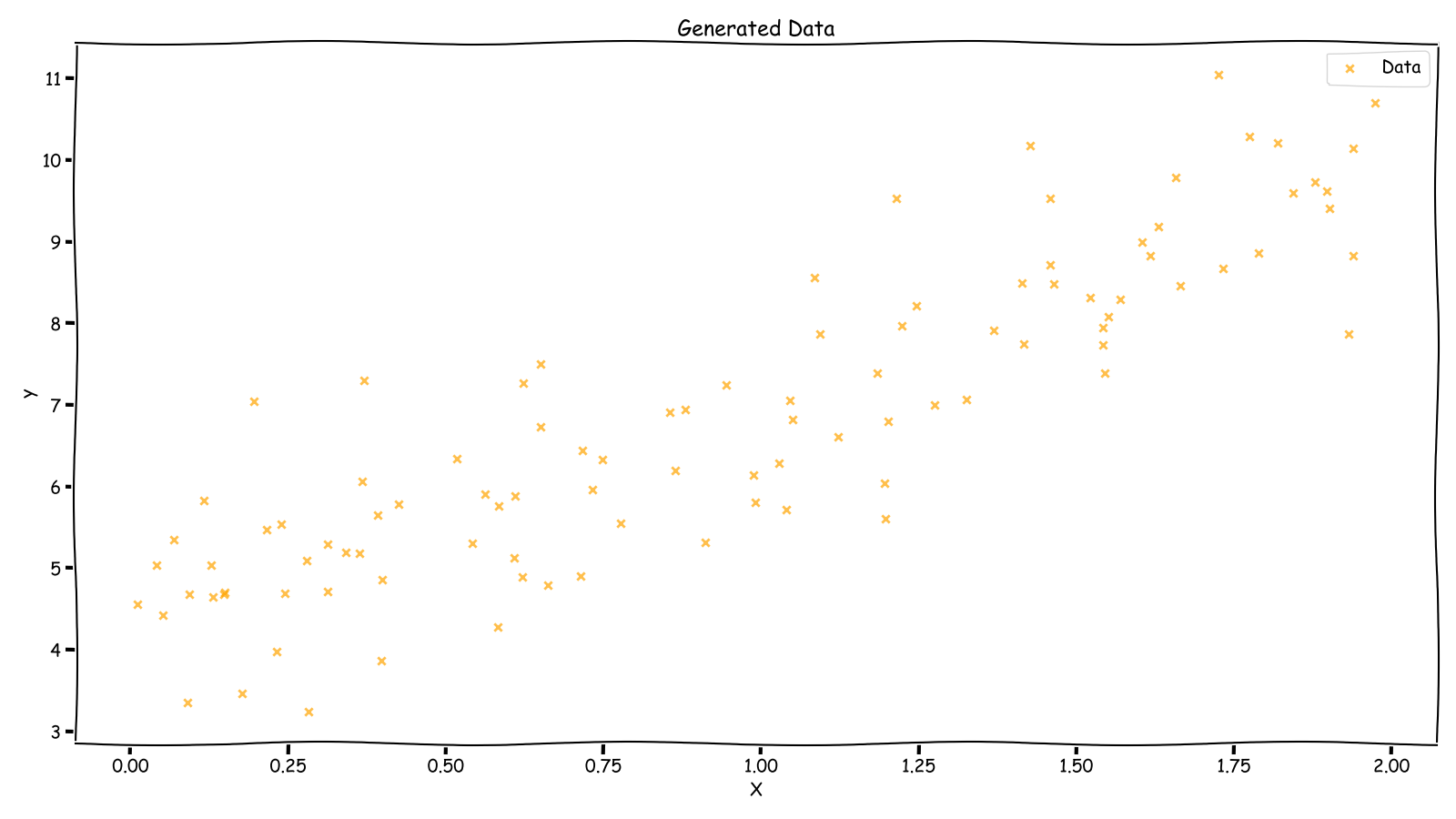Generated Data

---

🧠 Step 2: The Goal of Linear Regression

We want to find the best line:

y_pred = m * x + b

such that the line is as close as possible to all points.

But how do we define "closeness"?

---

📉 Step 3: Loss Function – Mean Squared Error (MSE)

The MSE is the average of squared differences between actual and predicted values.

python
def mean_squared_error(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

We aim to minimize this MSE.

---

🔁 Step 4: Gradient Descent (Updating m and b)

We use gradient descent to find optimal m and b.

python
# Initialize weights
m, b = 0.0, 0.0
learning_rate = 0.1
n_iterations = 100
n = len(X)

mse_list = []

for _ in range(n_iterations):
    y_pred = m * X + b
    error = y - y_pred

    # Calculate gradients
    m_grad = -2 * np.sum(X * error) / n
    b_grad = -2 * np.sum(error) / n

    # Update parameters
    m -= learning_rate * m_grad
    b -= learning_rate * b_grad

    # Track MSE
    mse = mean_squared_error(y, y_pred)
    mse_list.append(mse)

---

🧩 Step 5: Plotting the Final Line

python
# Final prediction
y_pred = m * X + b

plt.scatter(X, y, label="Data")
plt.plot(X, y_pred, color="red", label="Regression Line")
plt.title("Final Fitted Line")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.grid(True)
plt.show()

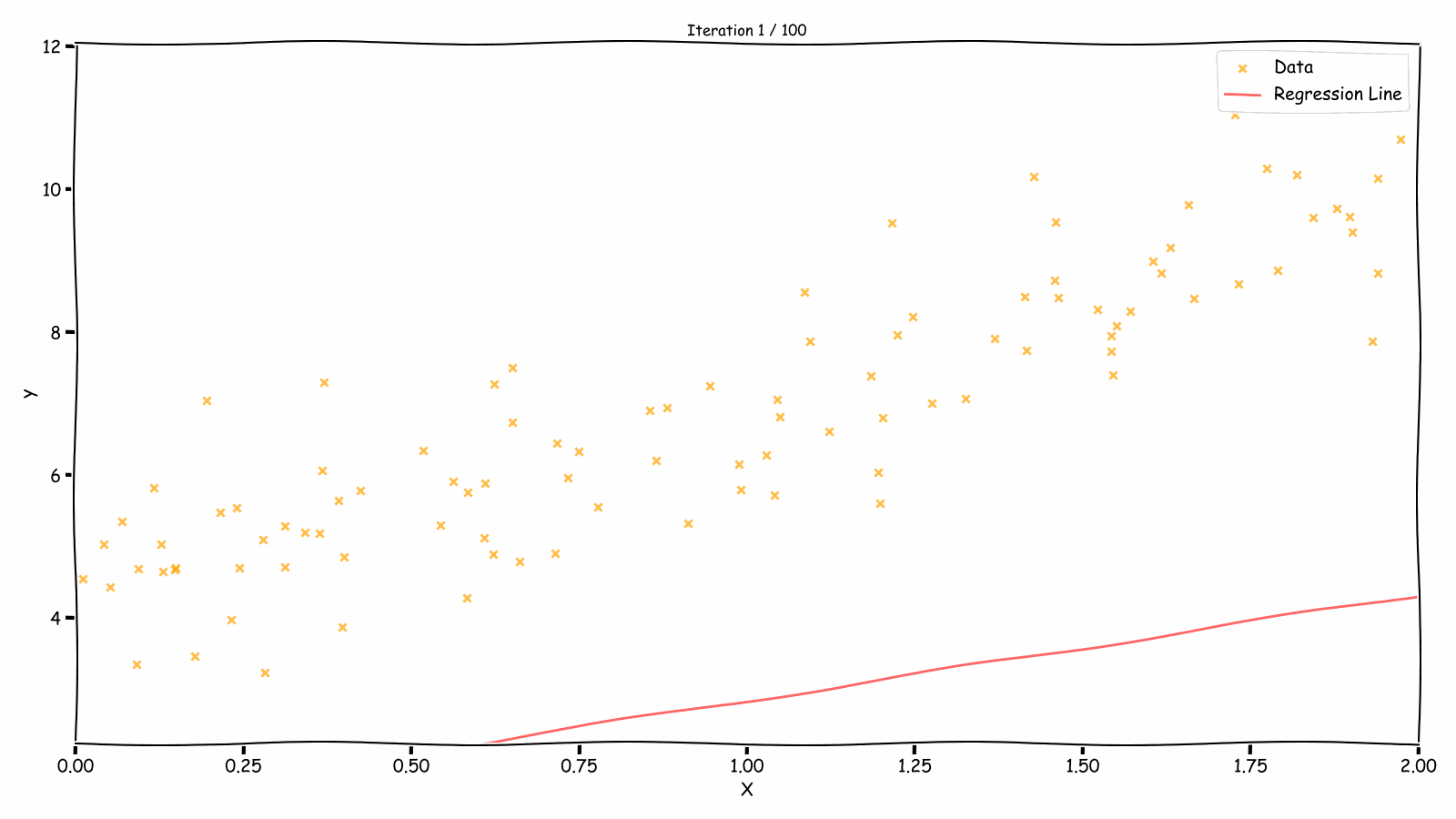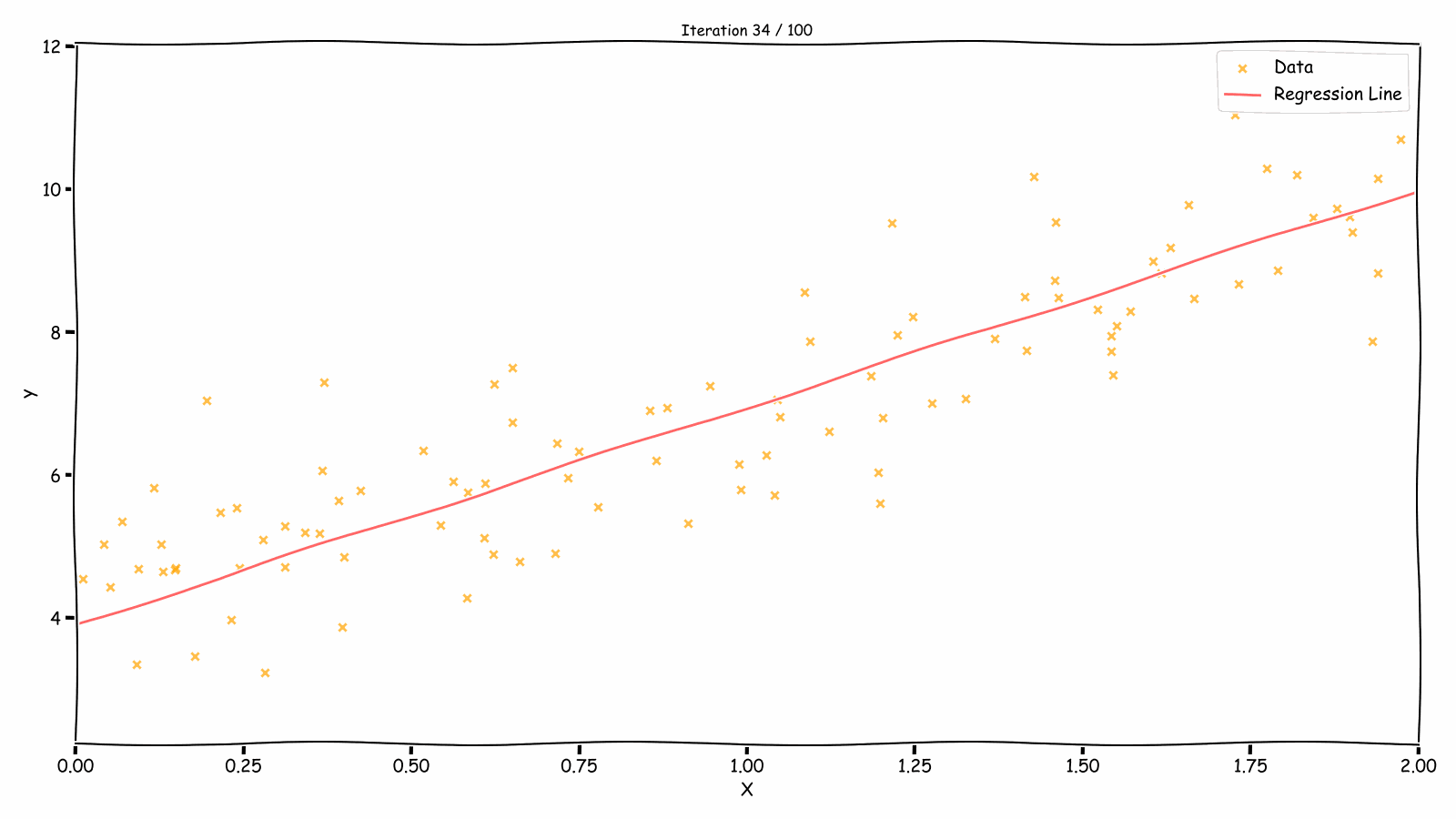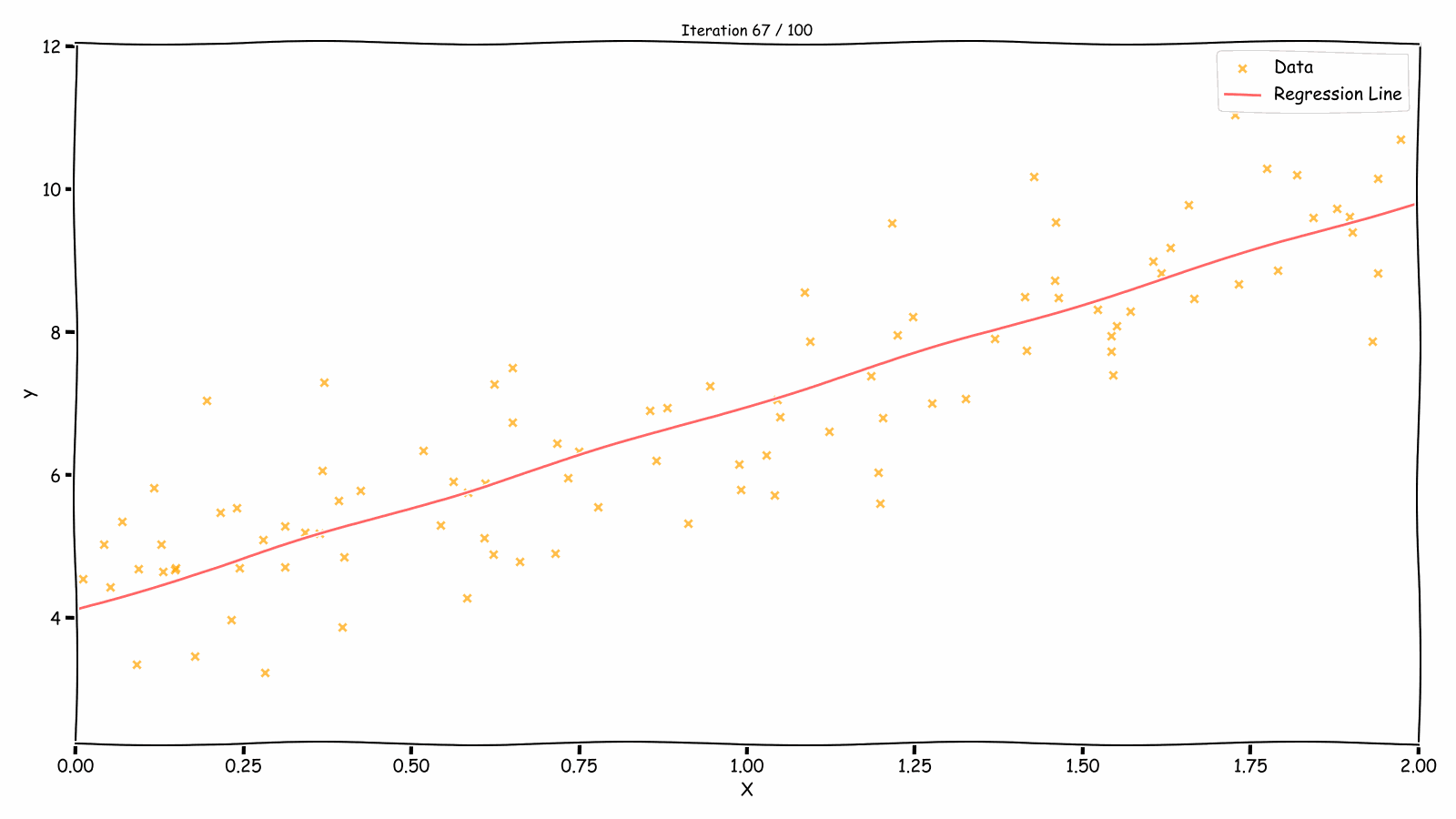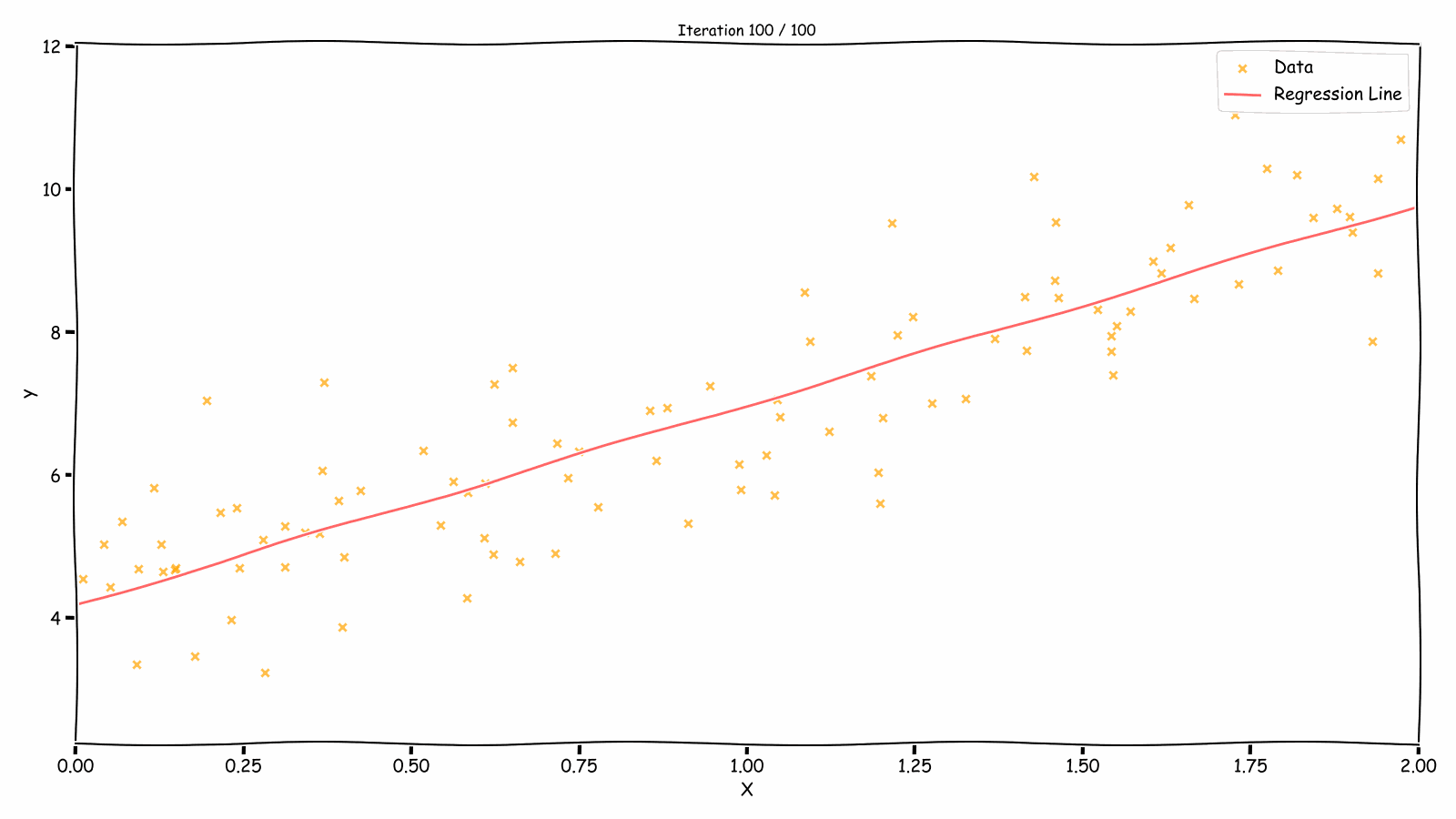Fitting Over Iterations

---

📈 Step 6: Visualizing Loss Over Iterations

python
plt.plot(range(n_iterations), mse_list, color='purple')
plt.title("Loss Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("MSE")
plt.grid(True)
plt.show()

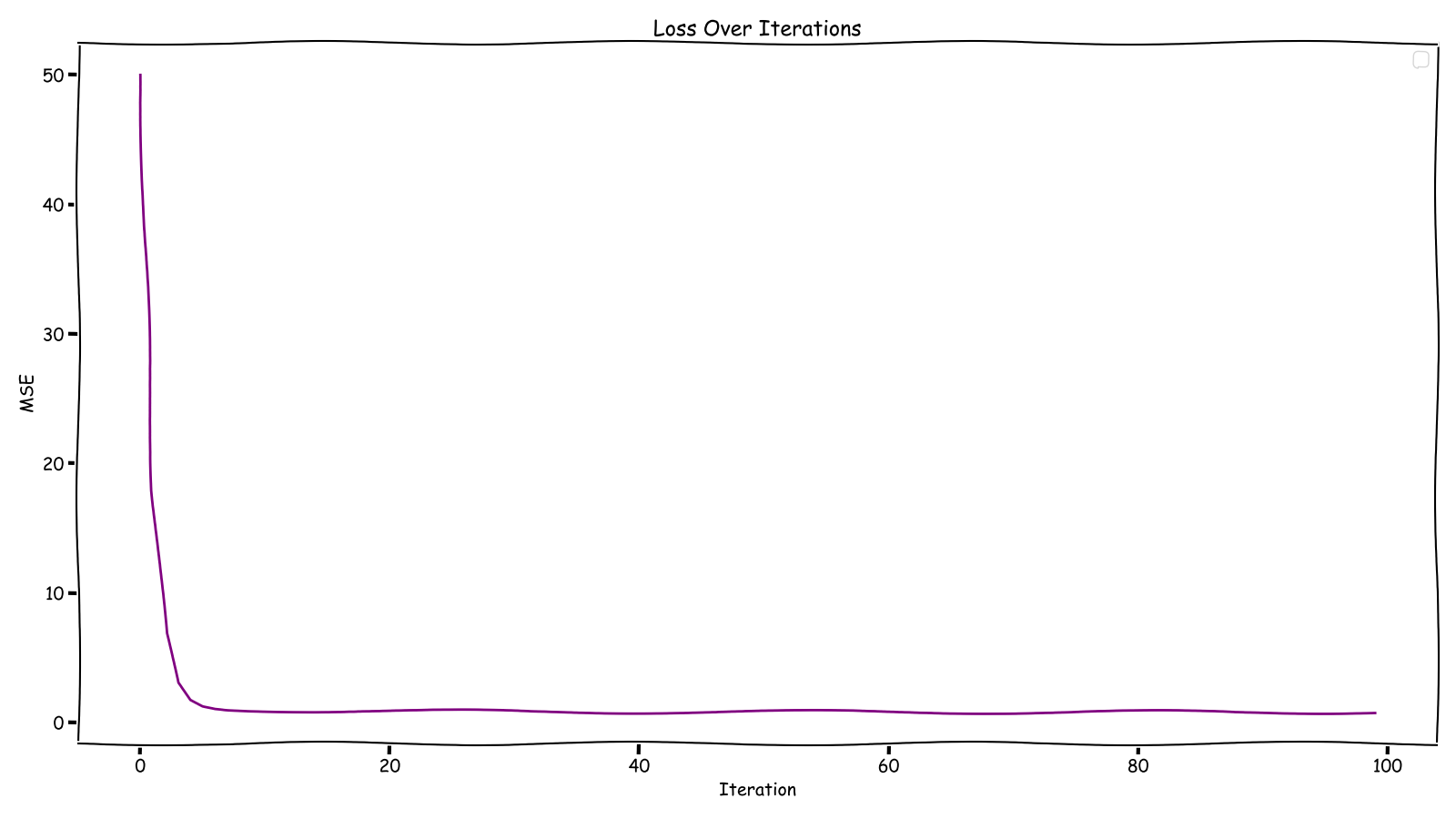Loss Over Iterations

---

✅ Conclusion

Linear Regression might be simple, but understanding it visually helps you internalize the ML workflow:

• Define a model
• Use a loss function
• Optimize parameters using gradient descent
• Visualize everything!

This same pattern applies to more complex algorithms too.